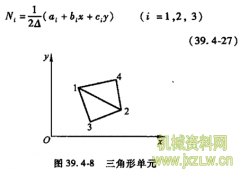
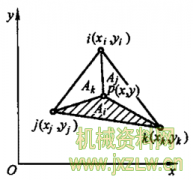
摘要:对于一个数值计算方法，一般总希望随着网格的逐步细分，所得到的解答能够收效于问题的精确解。根据前面的分析，在有限元中，一旦确定了单元的形状，位移模式的选择将是非常关键的。由于载荷的移置、应力矩阵和刚度矩阵的建立都依赖于单元的位移模式，所以，
对于一个数值计算方法，一般总希望随着网格的逐步细分，所得到的解答能够收效于问题的精确解。根据前面的分析，在有限元中，一旦确定了单元的形状，位移模式的选择将是非常关键的。由于载荷的移置、应力矩阵和刚度矩阵的建立都依赖于单元的位移模式，所以，如果所选择的位移模式与真实的位移分布有很大的差别，将会很难获得良好的数值解。
可以证明，对于一个给定的位移模式，其刚度系数的数值比精确值要大。所以，在给定的载荷之下.有限元计算模型的变形将比实际结构的变形小。因此细分单元网格，位移近似解将由下方收敛于精确解，即得到真实解的下界。
为了保证解答的收敛性，位移模式要满足以下三个条件，即
I)位移模式必须包含单元的刚体位移。也就是说，当节点位移由某个刚体位移引起时，弹性体内将不会产生应变。所以，位移模式不但要具有描述单元本身形变的能力，而且还要具有描述由于其他单元形变而通过节点位移引起单元刚体位移的能力。例如，平面三角形单元位移模式的常数项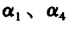
就是用于提供刚体位移的。
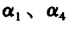就是用于提供刚体位移的。
2)位移模式必须能包含单元的常应变。每个单元的应变一般包含两个部分:一部分是与该单元中各点的坐标位置有关的应变，另一部分是与位置坐标无关的应变(即所谓的常应变)。从物理意义上看，当单元尺寸无限缩小时，每个单元中的应变应趋于常量。因此，在位移模式中必须包含这些常应变，否则就不可能使数值解收敛于正确解。很显然，在平面三角形单元的位移模式中，与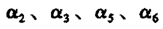
有关的线性项就是提供单元中的常应变的。
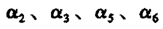有关的线性项就是提供单元中的常应变的。
3)位移模式在单元内要连续，且在相邻单元之间的位移必须协调。当选择多项式来构成位移模式时，单元内的连续性要求总是得到满足的，单元间的位移协调性，就是要求单元之间既不会出现开裂也不会出现重登的现象。通常，当单元交界面上的位移取决于该交界面上节点的位移时，就可以保证位移的协调性。
在有限元法中，把能够满足条件1和2的单元，称为完备单元;满足条件3的单元，称为协调单元或保续单元。前面讨论过的三角形单元和矩形单元，均能同时满足上述三个条件，因此都属于完备的协调单元。在某些梁、板及壳体分析中，要使单元满足条件3会比较困难，实践中有时也出现一些只满足条件1和2的单元，其收敛性往往也能够令人满意。放松条
件3的单元，即完备而不协调的单元，已获得了很多成功的应用。不协调单元的缺点主要是不能事先确定其刚度与真实刚度之间的大小关系。但不协调单元一般不像协调单元那样硬(即比较柔软)，因此有可能会比协调单元收敛得快。
在选择多项式作为单元的位移模式时，其阶次的确定要考虑解答的收敛性，即单元的完备性和协调性要求。实践证明，虽然这两项确实是所要考虑的重要因素，但并不是唯一的因素。选择多项式位移模式阶次时.需要考虑的另一个因素是.所选的模式应该与局部坐标系的方位无关，这一性质称为几何各向同性。对于线性多项式，各向同性的要求通常就等价于位移模式必须包含常应变状态;对于高次位移模式，就是不应该有一个偏移的坐标方向，也就是位移形式不应该随局部坐标的更换而改变。经验证明，实现几何各向同性的一种有效方法是，可以根据帕斯卡三角形来选择二维多项式的各项。在二维多项式中，如果包含有对称轴一边的某一项，就必须同时包含有另一边的对称项。
选择多项式位移模式时，还应考愈多项式中的项数必须等于或稍大于单元边界上的外节点的自由度数。通常取项数与单元的外节点的自由度数相等，取过多的项数是不恰当的。
(责任编辑：laugh521521)
上一篇：用面积坐标表达的形函数
下一篇：等效节点载荷列阵
| 文章分享： |
|
